Reaction-Diffusion Equation with a Time-dependent Dirichlet Boundary Condition on a Disk
In this tutorial, we consider a reaction-diffusion equation on a disk with a boundary condition of the form $\mathrm du/\mathrm dt = u$:
\[\begin{equation*} \begin{aligned} \pdv{u(r, \theta, t)}{t} &= \div[u\grad u] + u(1-u) & 0<r<1,\,0<\theta<2\pi,\\[6pt] \dv{u(1, \theta, t)}{t} &= u(1,\theta,t) & 0<\theta<2\pi,\,t>0,\\[6pt] u(r,\theta,0) &= \sqrt{I_0(\sqrt{2}r)} & 0<r<1,\,0<\theta<2\pi, \end{aligned} \end{equation*}\]
where $I_0$ is the modified Bessel function of the first kind of order zero. For this problem the diffusion function is $D(\vb x, t, u) = u$ and the source function is $R(\vb x, t, u) = u(1-u)$, or equivalently the force function is
\[\vb q(\vb x, t, \alpha,\beta,\gamma) = \left(-\alpha(\alpha x + \beta y + \gamma), -\beta(\alpha x + \beta y + \gamma)\right)^{\mkern-1.5mu\mathsf{T}}.\]
As usual, we start by generating the mesh.
using FiniteVolumeMethod, DelaunayTriangulation, ElasticArrays
r = 1.0
circle = CircularArc((0.0, r), (0.0, r), (0.0, 0.0))
points = NTuple{2, Float64}[]
boundary_nodes = [circle]
tri = triangulate(points; boundary_nodes)
A = get_area(tri)
refine!(tri; max_area=1e-4A)
mesh = FVMGeometry(tri)FVMGeometry with 8873 control volumes, 17488 triangles, and 26360 edgesusing CairoMakie
triplot(tri)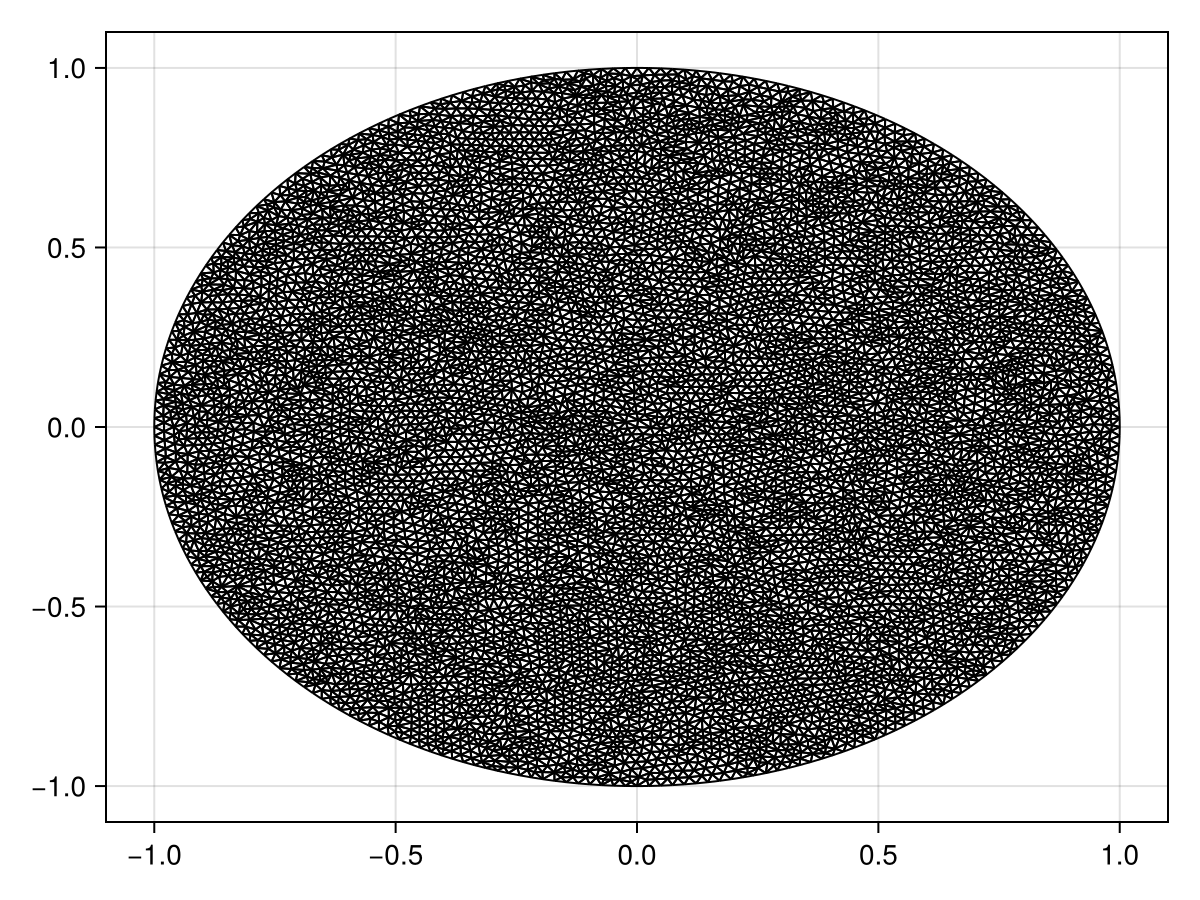
Now we define the boundary conditions and the PDE.
using Bessels
BCs = BoundaryConditions(mesh, (x, y, t, u, p) -> u, Dudt)BoundaryConditions with 1 boundary condition with type Dudtf = (x, y) -> sqrt(besseli(0.0, sqrt(2) * sqrt(x^2 + y^2)))
D = (x, y, t, u, p) -> u
R = (x, y, t, u, p) -> u * (1 - u)
initial_condition = [f(x, y) for (x, y) in DelaunayTriangulation.each_point(tri)]
final_time = 0.10
prob = FVMProblem(mesh, BCs;
diffusion_function=D,
source_function=R,
final_time,
initial_condition)FVMProblem with 8873 nodes and time span (0.0, 0.1)We can now solve.
using OrdinaryDiffEq, LinearSolve
alg = FBDF(linsolve=UMFPACKFactorization(), autodiff=false)
sol = solve(prob, alg, saveat=0.01)retcode: Success
Interpolation: 1st order linear
t: 11-element Vector{Float64}:
0.0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
u: 11-element Vector{Vector{Float64}}:
[1.2514323512504983, 1.2514323512504983, 1.2514323512504983, 1.2514323512504983, 1.2514323512504983, 1.2514323512504983, 1.2514323512504983, 1.2514323512504983, 1.0, 1.0732643239064652 … 1.1273707895718001, 1.1385143775820408, 1.0759864640747345, 1.1059360537374112, 1.1644440100218003, 1.086951026267742, 1.0392678506023625, 1.1024192941416517, 1.0375448554959907, 1.0285121494474723]
[1.2640100706601904, 1.2640100706601904, 1.2640100706601904, 1.2640100706601904, 1.2640100706601904, 1.2640100706601904, 1.2640100706601904, 1.2640100706601904, 1.010072827189627, 1.0840429983811803 … 1.1386913162958587, 1.149957061010934, 1.0867342657053447, 1.1169954229882637, 1.1761491484349387, 1.097859724767572, 1.0496225602041886, 1.1134630272401507, 1.0479083282749462, 1.038846361413745]
[1.2767133753205482, 1.2767133753205482, 1.2767133753205482, 1.2767133753205482, 1.2767133753205482, 1.2767133753205482, 1.2767133753205482, 1.2767133753205482, 1.0201621346069185, 1.0949624362253318 … 1.1501712735649283, 1.1615092285119466, 1.0978235745798774, 1.1283477592432116, 1.1879807677713294, 1.1089288000967408, 1.0603916931545947, 1.124742830768333, 1.0586117277808862, 1.04929929434763]
[1.2895470812374505, 1.2895470812374505, 1.2895470812374505, 1.2895470812374505, 1.2895470812374505, 1.2895470812374505, 1.2895470812374505, 1.2895470812374505, 1.0302769580624629, 1.1060262035665385 … 1.1618070740543525, 1.173168776362545, 1.109231353099996, 1.139967416030438, 1.1999400241760072, 1.1201487193063064, 1.0715360938160452, 1.1362395685639237, 1.0696381989450243, 1.059873902824769]
[1.302510632039605, 1.302510632039605, 1.302510632039605, 1.302510632039605, 1.302510632039605, 1.302510632039605, 1.302510632039605, 1.302510632039605, 1.0406910239371934, 1.1171091340294794 … 1.1735041893784472, 1.1849774582790669, 1.1202090397005329, 1.1512823749273153, 1.2120359853107288, 1.131406138233007, 1.0820746482895307, 1.1475905448161863, 1.0801637764882925, 1.070519521834062]
[1.315601733019956, 1.315601733019956, 1.315601733019956, 1.315601733019956, 1.315601733019956, 1.315601733019956, 1.315601733019956, 1.315601733019956, 1.0513706650882881, 1.1282780250213813 … 1.1851012263164016, 1.1969033695731055, 1.1309450340071918, 1.1624958725070047, 1.2241216320974937, 1.1426225956459146, 1.0922807175431986, 1.1588280993929778, 1.0905688200744732, 1.0812393966206195]
[1.3288227397687316, 1.3288227397687316, 1.3288227397687316, 1.3288227397687316, 1.3288227397687316, 1.3288227397687316, 1.3288227397687316, 1.3288227397687316, 1.0620077182715573, 1.1396006997295407 … 1.196942268652137, 1.208938556288962, 1.1421522529613672, 1.1740758929571402, 1.2363870325219126, 1.1540557105206874, 1.1030573284413607, 1.1703828593696526, 1.1013980028119512, 1.092093270997209]
[1.342176251960254, 1.342176251960254, 1.342176251960254, 1.342176251960254, 1.342176251960254, 1.342176251960254, 1.342176251960254, 1.342176251960254, 1.0726217754162966, 1.1510675668098194 … 1.2090337744979405, 1.2210874003539933, 1.1537725807771724, 1.1859720035183838, 1.2488446449424317, 1.1657033924531646, 1.1143244743472278, 1.1822298312494852, 1.1125783718277082, 1.103079931118372]
[1.3556643720524755, 1.3556643720524755, 1.3556643720524755, 1.3556643720524755, 1.3556643720524755, 1.3556643720524755, 1.3556643720524755, 1.3556643720524755, 1.0833148130050658, 1.1626569176890338 … 1.2212717115214704, 1.2333534400505348, 1.165568042669753, 1.1980229560494489, 1.2614406141052927, 1.1774846278605902, 1.1257773315521045, 1.1942275748890694, 1.1239223371804457, 1.1141822141824753]
[1.3692876325241807, 1.3692876325241807, 1.3692876325241807, 1.3692876325241807, 1.3692876325241807, 1.3692876325241807, 1.3692876325241807, 1.3692876325241807, 1.0941466581849084, 1.1743582718866132 … 1.2335865503669432, 1.245739480469627, 1.1774091160706128, 1.210147848354348, 1.2741355030441712, 1.1893496358715718, 1.1372534190597219, 1.2062968834779801, 1.1353373008760794, 1.1253896102037906]
[1.3830464198485353, 1.3830464198485353, 1.3830464198485353, 1.3830464198485353, 1.3830464198485353, 1.3830464198485353, 1.3830464198485353, 1.3830464198485353, 1.1051771397053842, 1.1861479297293884 … 1.2459561635443703, 1.258261077078496, 1.1891564927425846, 1.2222494417041094, 1.286927897517785, 1.2012796200666334, 1.1485733838430376, 1.2183733302700932, 1.1466673538441456, 1.13669250180302]fig = Figure(fontsize=38)
for (i, j) in zip(1:3, (1, 6, 11))
ax = Axis(fig[1, i], width=600, height=600,
xlabel="x", ylabel="y",
title="t = $(sol.t[j])",
titlealign=:left)
tricontourf!(ax, tri, sol.u[j], levels=1:0.01:1.4, colormap=:matter)
tightlimits!(ax)
end
resize_to_layout!(fig)
fig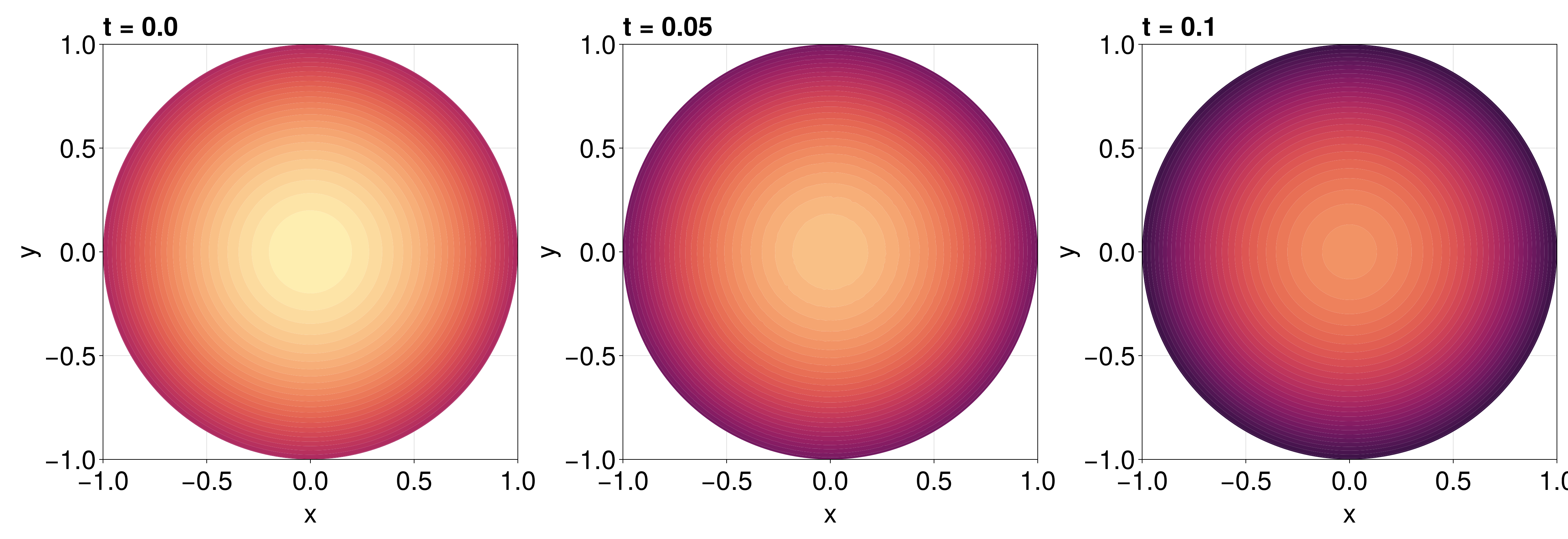
Just the code
An uncommented version of this example is given below. You can view the source code for this file here.
using FiniteVolumeMethod, DelaunayTriangulation, ElasticArrays
r = 1.0
circle = CircularArc((0.0, r), (0.0, r), (0.0, 0.0))
points = NTuple{2, Float64}[]
boundary_nodes = [circle]
tri = triangulate(points; boundary_nodes)
A = get_area(tri)
refine!(tri; max_area=1e-4A)
mesh = FVMGeometry(tri)
using CairoMakie
triplot(tri)
using Bessels
BCs = BoundaryConditions(mesh, (x, y, t, u, p) -> u, Dudt)
f = (x, y) -> sqrt(besseli(0.0, sqrt(2) * sqrt(x^2 + y^2)))
D = (x, y, t, u, p) -> u
R = (x, y, t, u, p) -> u * (1 - u)
initial_condition = [f(x, y) for (x, y) in DelaunayTriangulation.each_point(tri)]
final_time = 0.10
prob = FVMProblem(mesh, BCs;
diffusion_function=D,
source_function=R,
final_time,
initial_condition)
using OrdinaryDiffEq, LinearSolve
alg = FBDF(linsolve=UMFPACKFactorization(), autodiff=false)
sol = solve(prob, alg, saveat=0.01)
fig = Figure(fontsize=38)
for (i, j) in zip(1:3, (1, 6, 11))
ax = Axis(fig[1, i], width=600, height=600,
xlabel="x", ylabel="y",
title="t = $(sol.t[j])",
titlealign=:left)
tricontourf!(ax, tri, sol.u[j], levels=1:0.01:1.4, colormap=:matter)
tightlimits!(ax)
end
resize_to_layout!(fig)
figThis page was generated using Literate.jl.